12 분 소요

1. 딥러닝이란?

1) 머신러닝과 딥러닝의 차이

image

  • 📌출처 : kt 엔터프라이즈

  • Deeplearning은 Machinelearning의 일종
  • 인간의 두뇌, 즉 신경망에 영감을 얻은 학습 방식


2) 단층 퍼셉트론(Single-layer Perceptron) : 하나의 신경망

그림1.jpg

$$ y = \begin{cases} 0 & (w_1 x_1 + w_2 x_2 \le \theta) \\ 1 & (w_1 x_1 + w_2 x_2 > \theta) \end{cases} $$
  • 다수의 신호를 입력 받아 하나의 신호로 출력(임계 값θ을 기준으로 출력 여부 결정)
    • 신호 x가 가중치 w를 만나 y의 출력을 결정하는 구조


✨ 단층 퍼셉트론의 한계 : 선형성(XOR게이트 구현 불가)

  • AND게이트
x1 x2 y
0 0 0
1 0 0
0 1 0
1 1 1
  • NAND게이트
x1 x2 y
0 0 1
1 0 1
0 1 1
1 1 0 
x1 = list(range(-1, 3))
x2 = list(map(lambda x:-x + 1.5, x1))

import matplotlib.pyplot as plt
plt.axhline(0, color='black',linewidth=1)
plt.axvline(0, color='black',linewidth=1)
plt.plot(x1, x2)
plt.scatter(0, 0, color='red', marker="o", label="(0,0)")
plt.scatter(1, 0, color='green', marker="o", label="(1,0)")
plt.scatter(0, 1, color='black', marker="o", label="(0,1)")
plt.scatter(1, 1, color='blue', marker="o", label="(1,1)")
plt.legend()
plt.xlabel("X1")
plt.ylabel("X2")
plt.fill([max(x1),max(x1), min(x1)],[2.5,-0.5,2.5],alpha=0.3) # AND 게이트
plt.fill([min(x1),min(x1), max(x1)],[-0.5,2.5,-0.5],alpha=0.1) # NAND 게이트

[<matplotlib.patches.Polygon at 0x2499d02b350>]


  • OR게이트
x1 x2 y
0 0 0
1 0 1
0 1 1
1 1 1 
x1 = list(range(-1, 3))
x2 = list(map(lambda x:-x + 0.5, x1))

import matplotlib.pyplot as plt
plt.axhline(0, color='black',linewidth=1)
plt.axvline(0, color='black',linewidth=1)
plt.plot(x1, x2)
plt.scatter(0, 0, color='red', marker="o", label="(0,0)")
plt.scatter(1, 0, color='green', marker="o", label="(1,0)")
plt.scatter(0, 1, color='black', marker="o", label="(0,1)")
plt.scatter(1, 1, color='blue', marker="o", label="(1,1)")
plt.legend()
plt.xlabel("X1")
plt.ylabel("X2")
plt.fill([min(x1),min(x1), max(x1)],[-1.5,1.5,-1.5],alpha=0.1) # OR 게이트

[<matplotlib.patches.Polygon at 0x2499e2ea950>]


  • XOR 게이트(✨ 구현 불가)
x1 x2 y
0 0 0
1 0 1
0 1 1
1 1 0 
x1 = list(range(-1, 3))
x2 = list(map(lambda x:-x + 1, x1))

import matplotlib.pyplot as plt
plt.axhline(0, color='black',linewidth=1)
plt.axvline(0, color='black',linewidth=1)
plt.plot(x1, x2)
plt.scatter(0, 0, color='red', marker="x", label="0")
plt.scatter(1, 0, color='blue', marker="o", label="1")
plt.scatter(0, 1, color='blue', marker="o")
plt.scatter(1, 1, color='red', marker="x")
plt.legend()
plt.xlabel("X1")
plt.ylabel("X2")
plt.fill([min(x1),min(x1), max(x1)],[-1.0,2,-1],alpha=0.1) # XOR 게이트

[<matplotlib.patches.Polygon at 0x249a396ec90>]


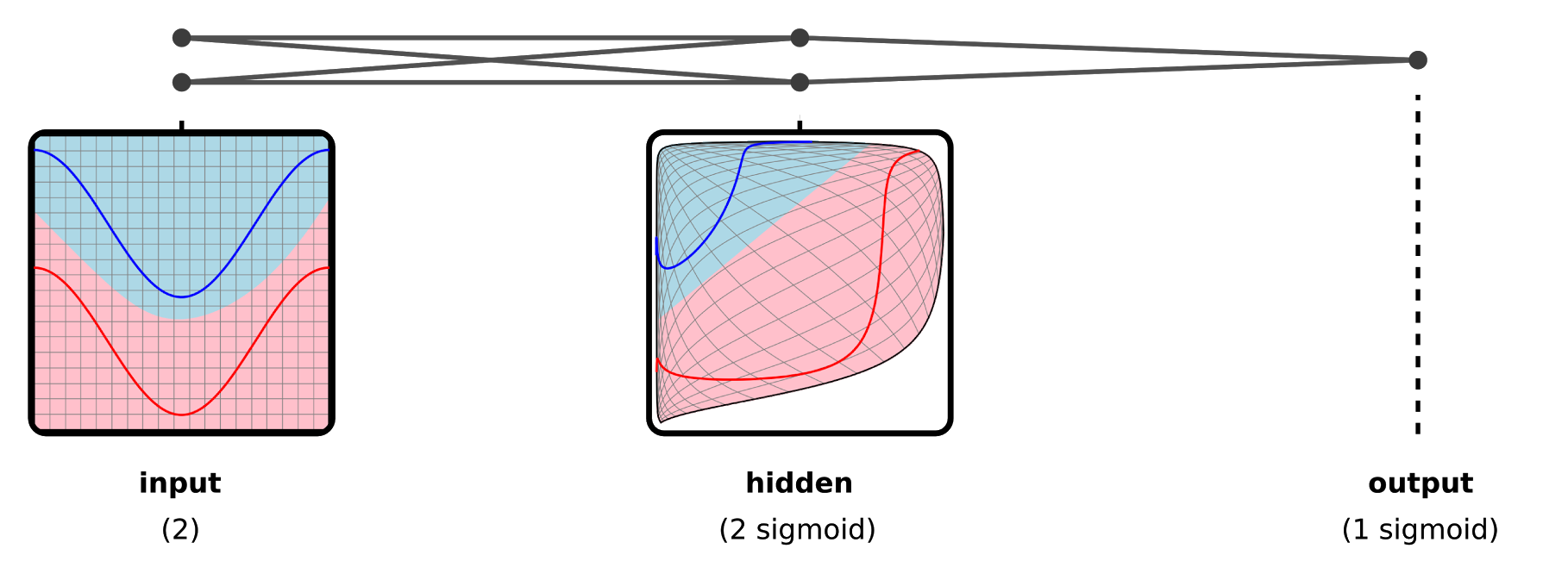
3) 다층 퍼셉트론(Multi-layer Perceptron) : 여러 개의 신경망

image

  • 현재 딥러닝의 기본적인 구조
  • 입력층과 출력층 사이에 다수의 은닉층, 가중치들이 존재(비선형성 갖춤)

image


2. 딥러닝의 학습 방법

1) 활성화 함수(Activation Function)

  • 임계값θ 대신 활용하여 비선형성을 확보한 방법

image

  • 📌출처 : 위키피디아


(1) 활성화 함수(Activation Function)의 종류

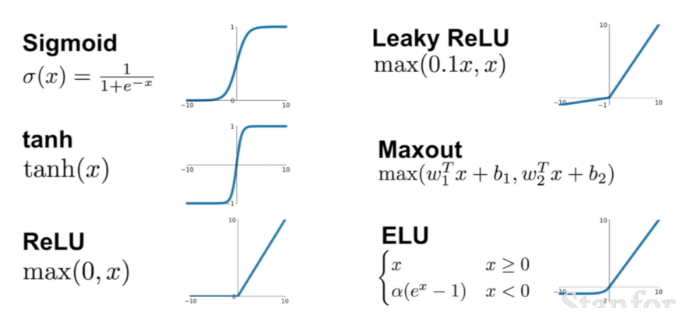
image


  • 계단(step) 함수(0, 1 : 이진분류)
    • 단점 : 미분 불가능 → 경사하강법 이용 불가(사실상 거의 이용하지 않음)
$$ y = \begin{cases} 0 & (x < 0) \\ 1 & (x > 0) \end{cases} $$ 
import numpy as np
import matplotlib.pylab  as plt

## 함수 구현
def step_function(x):
    return np.array(x>0, dtype=int)

## 그래프
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.show()


  • 시그모이드(Sigmoid) 함수(0~1 : T/F확률)
    • 계단함수를 미분 가능하도록 개선한 방식, 주로 이진 분류 출력층에 사용.
    • 단점 : 기울기 소실 → 입력값이 매우 크거나 작으면 기울기가 0에 가까워져 (경사하강법을 이용한) 학습 속도가 느려짐
$$ sigmoid(x) = \frac{1}{1 + e^{-x}} $$
import numpy as np
import matplotlib.pylab  as plt

## 함수 구현
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

## 그래프
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.show()



## 도함수 그래프
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)*(1-sigmoid(x))
plt.plot(x,y)
plt.ylim(-0.1, 1.1)
plt.show()


  • 하이퍼볼릭 탄젠트(Tanh) 함수(-1~1)
    • 시그모이드 함수의 출력값 표현력을 개선한 모델
    • 단점 : 기울기 소실 → 입력값이 매우 크거나 작으면 기울기가 0에 가까워짐(단, sigmoid보단 개선됨)
$$ tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$$
import numpy as np
import matplotlib.pylab  as plt

## 함수 구현
def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

## 그래프
x = np.arange(-5.0, 5.0, 0.1)
y = tanh(x)
plt.plot(x,y)
plt.show()



## 도함수 그래프
x = np.arange(-5.0, 5.0, 0.1)
y = (1 - tanh(x))*(1 + tanh(x))
plt.plot(x,y)
plt.ylim(-0.1, 1.1)
plt.show()


  • 렐루(ReLu) 함수(0, x : 양수면 자기 값)
    • 기울기 소실 문제 개선(단, 음수 입력값에 대한 정보 손실), 주로 은닉층에 사용.
    • 단점 : 음수에 대한 기울기 소실 → 0보다 작은 수에 대해 기울기 0
$$f(x) = max(0, x)$$ 
import numpy as np
import matplotlib.pylab  as plt

## 함수 구현
def relu(x):
    return np.maximum(0,x)

## 그래프 그리기
x = np.arange(-5.0, 5, 1)
y = relu(x)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x249a4d20950>]


  • 리키 렐루(Leaky ReLu) 함수
    • ReLu함수의 음수 입력값에 대한 정보 손실 개선
$$f(x) = max(0.01x, x)$$ 
import numpy as np
import matplotlib.pylab  as plt

## 함수 구현
def relu(x):
    return np.maximum(0.01*x,x)

## 그래프 그리기
x = np.arange(-5.0, 5, 0.01)
y = relu(x)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x249a50febd0>]


  • 소프트맥스(softmax) 함수(0~1 : 클래스별 확률)
    • 전체 합산이 1, 주로 다중 클래스 출력층에 사용.
    • 단점
      • 기울기 폭발 → 입력 값이 클수록 급격하게 기울기 상승
      • 기울기 소실 → 입력 값이 작을 수록 기울기 소실
$$softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}$$
def softmax(x):
    exp_x = np.exp(x)
    sum_exp_x = np.sum(exp_x)
    y = exp_x / sum_exp_x
    return y

## 그래프 그리기
x = np.arange(-5.0, 5, 0.1)
y = softmax(x)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x249a5168b50>]


2) 순전파(Feedfoward)와 역전파(Backpropagation)

  • 순전파 정의 : 입력층에서 출력층 방향으로 이동하면서 은닉층에서 가중치w가 곱해져 최종 결과가 출력되는 과정
    • ✨ 가중치w는 첫 순전파때 랜덤하게 배정된 뒤 여러 차례의 역전파-순전파를 통해 조정된다.
  • 역전파 정의 : 출력층 값을 활용하여 가중치w를 조정하는 과정
    • ✨ 출력값과 실제값을 활용하여 손실함수(Loss Function)을 정의하고, 경사하강법(미분 값을 활용)을 통해 가중치 w를 조정

image


(1) 손실함수(Loss Function) : 역전파(Backpropagation)의 기준

  • ✨어째서 정확도(accuracy)를 기준으로 쓰지 않는 걸까?
    • 기울기 계산의 어려움 : 크게 변동될 수 있거나, 변동하지 않을 수 있기 때문


  • MSE(Mean Squared Error)
    • 예측한 값과 실제 값 사이의 평균 제곱 오차(회귀분석)
$$ MSE = \frac{1}{N}\sum^{N}_{i=1}{(y_{i}-\hat{y_{i}})^{2}} $$

y : 실제값
$\hat{y}$ : 예측값
N : 데이터수


  • RMSE(Root Mean Squared Error)
    • MSE 오류의 제곱을 구하기 때문에 값 왜곡을 줄이기 위해 루트를 씌운 값(회귀분석)
$$ RMSE = \sqrt{\frac{1}{N}\sum^{N}_{i=1}{(y_{i}-\hat{y_{i}})^{2}}} $$

y : 실제값
$\hat{y}$ : 예측값
N : 데이터수


  • Binary Crossentropy
    • 실제 레이블과 예측 레이블 간의 교차 엔트로피 손실을 계산(이진 분류)
$$ BCE = \frac{1}{N} \sum^{N}_{i=1}{-(y_{i}*log(p_{i})+(1-y_{i})*log(1-p_{i}))} $$

$y_{i}$ : 실제값
$p_{i}$ : 예측한 확률
N : 데이터수


  • Categorical Crossentropy
    • 실제 레이블과 예측 레이블 간의 교차 엔트로피 손실을 계산(다중 클래스 분류 + 원핫 인코딩)
$$ L = -\frac{1}{N} \sum^{N}_{j=1} \sum^{C}_{i=1} y_{ij}*log(p_{ij}) $$

$y_{ij}$ : 실제값
$p_{ij}$ : 예측한 확률
N : 데이터수
C : 클래스수


  • Sparse Categorical Crossentropy
    • 실제 레이블과 예측 레이블 간의 교차 엔트로피 손실을 계산(다중 클래스 분류 + 라벨 인코딩)


  • 원핫 인코딩 vs 라벨 인코딩

image


(2) 옵티마이저(Optimizer) : 역전파(Backpropagation) 시 가중치 조정 방법

  • 정의 : 손실함수(Loss function)의 가중치w에 대한 미분값을 활용하여 최소값을 찾아가는 방법

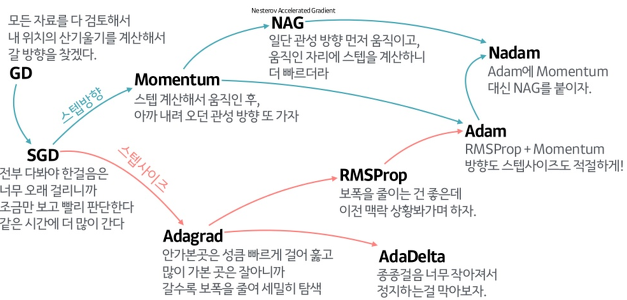
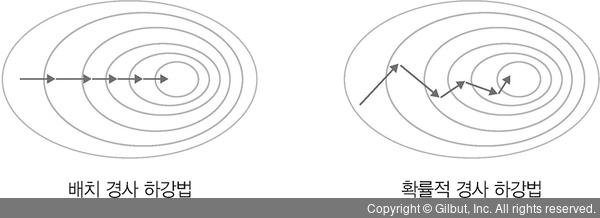
image


  • 발전방향

image


  • GD(경사 하강법)
    • 전체 데이터에 대해 가중치 조절
    • 단점 : 리소스 사용 과다
  • SGD(확률적 경사 하강법)
    • 랜덤하게 추출한 일부 데이터에 대해 가중치 조절
    • 장점 : 빠르다.
    • 단점 : 전역적 극소점(Global minima)을 못찾을 수 있다.
$$W_{t+1} = W_{t} - \alpha \frac{\partial L}{\partial W_{t}} $$

t : 시점
α : 학습률
W : 가중치
L : 손실함수

image


  • Momentum
    • SGD + 모멘텀(이전의 학습결과 반영)
    • 장점 : SGD보다 빠르다, 국지적 극소점(Local minima)에 빠지는 것을 피할 수 있다.
    • 단점 : 전역적 극소점(Global minima)에서 발산할 수 있다.
$$ v_{t} ← \alpha v_{t-1} - \eta \frac{\partial L}{\partial W_{t}} $$
$$W_{t+1} ← W_{t} + v_{t} $$

t : 시점
v : 관성계수
α : 관성계수 감쇠율 $\approx$ 0.9
η : 학습률
W : 가중치
L : 손실함수


  • AdaGrad
    • SGD + 학습률 감소(과거의 기울기 제곱)
    • 장점 : 안정적인 학습 가능하도록 함
    • 단점 : 학습이 길어지면 학습률이 0에 도달(국지적 극소점(Local minima)에 그칠 수 있다)
$$ h_{t} ← h_{t-1} + \frac{\partial L}{\partial W_{t}} ⊙ \frac{\partial L}{\partial W_{t}}$$
$$W_{t+1} ← W_{t} - \eta \frac{1}{\sqrt{h}_{t}} \frac{\partial L}{\partial W_{t}}$$

t : 시점
h : 학습률 조정 값
⊙ : 행렬의 원소별 곱셈
η : 학습률
W : 가중치
L : 손실함수


  • RMSProp
    • SGD + 학습률 감소(과거의 기울기 지수이동평균)
    • 한계 : AdaGrad의 단점의 완전히 해소하지 못함
$$ h_{t} ← ph_{t-1} + (1-p)\frac{\partial L}{\partial W_{t}} ⊙ \frac{\partial L}{\partial W_{t}}$$
$$W_{t+1} ← W_{t} - \eta \frac{1}{\sqrt{h_{t}}} \frac{\partial L}{\partial W_{t}}$$

t : 시점
p : 지수이동평균(0~1)
h : 학습률 조정 값
⊙ : 행렬의 원소별 곱셈
η : 학습률
W : 가중치
L : 손실함수


  • Adam✨✨
    • Momentum, RMSProp 융합한 기법(✨✨관성과 학습률 조정을 동시에 하는 기법)
    • ✨현 최고의 Optimizer
$$ m_{t} = \beta_{1}m_{t-1}+(1-\beta_{1})\frac{\delta L}{\delta W_{t}} $$
$$ v_{t} = \beta_{2}v_{t-1}+(1-\beta_{2}) \frac{\delta L}{\delta W_{t}} ⊙ \frac{\delta L}{\delta W_{t}}$$
$$ \hat{m_{t}} = \frac{m_{t}}{1-\beta^{t}_{1}}\quad \hat{v_{t}} = \frac{v_{t}}{1-\beta^{t}_{2}} $$
$$ W_{t+1} = W_{t} - \eta \frac{\hat{m_{t}}}{\sqrt{\hat{v_{t}}+\epsilon}} $$

t : 시점
m : 관성계수
$\beta_{1}$ : 관성계수의 지수이동평균 $\approx$ 0.9
$ \hat{m} $ : 관성계수의 가중평균식
v : 학습률 조정 값
$\beta_{2}$ : 학습률 조정 값의 지수이동평균 $\approx$ 0.999
$ \hat{v} $ : 학습률 조정 값의 가중평균식
⊙ : 행렬의 원소별 곱셈
η : 학습률
W : 가중치
L : 손실함수


  • 성능비교✨✨

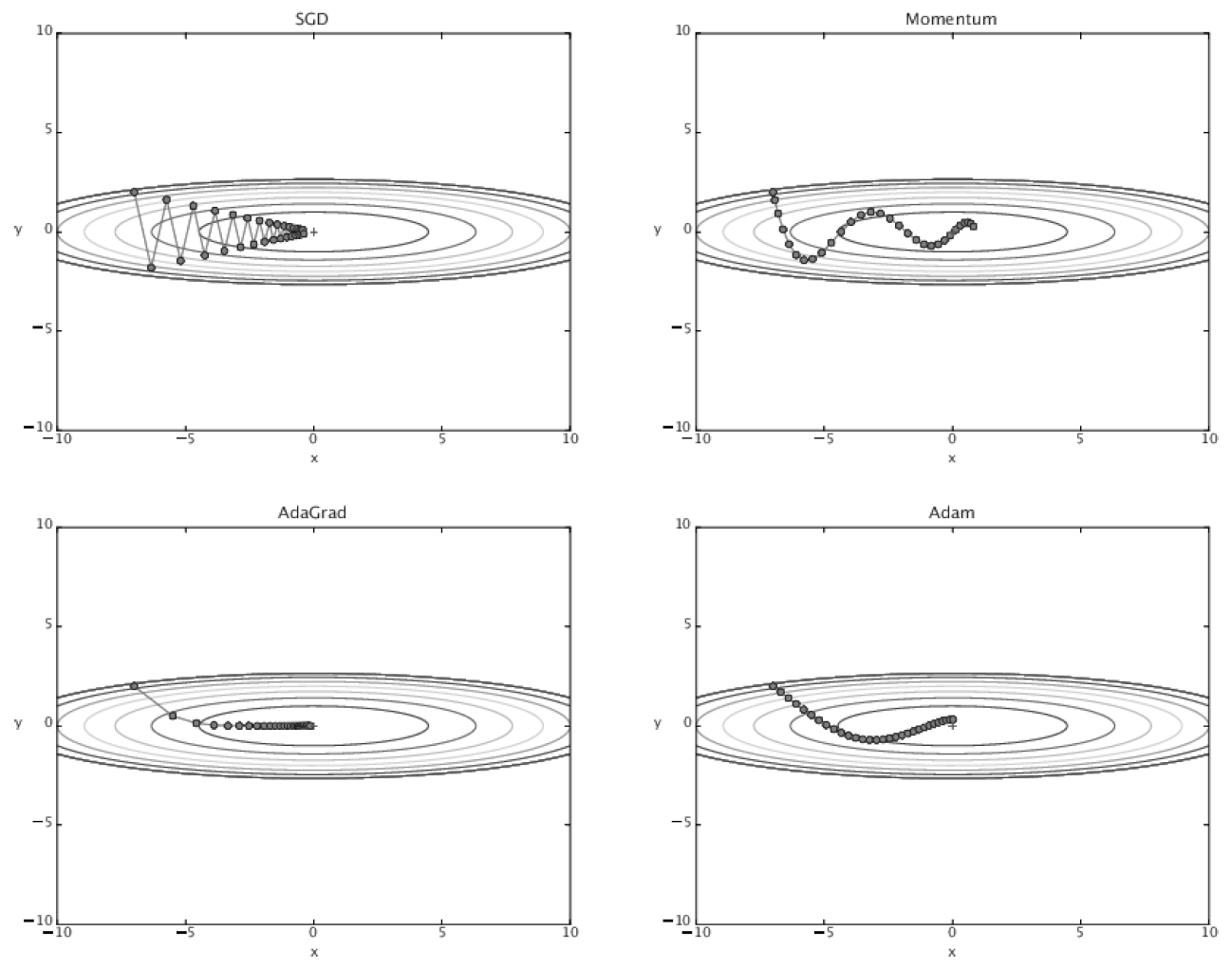
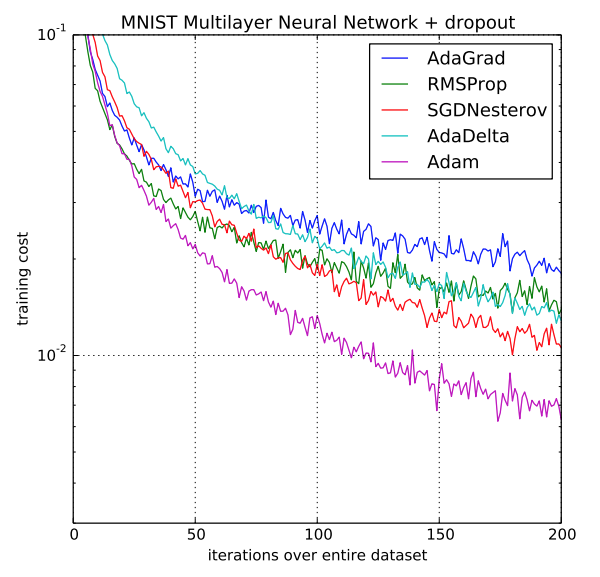
image

image


  • 극소점을 찾는 모습 코드 구현(Adam)
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import matplotlib.animation as animation

fig =plt.figure()
ax = plt.axes(xlim=(-10,10))
start_x = -8
learning_rate=1.3

## loss_function
def loss_function(x) :
    return (1/200)*(x-9)*(x)*(x+1)*(x+6) + 4

## loss_function's gradient
def loss_gradient(x) :
    return (1/100)*(2*np.power(x, 3)-3*np.power(x, 2)-57*x-27)

xrange = np.arange(-10,10,0.1)
loss_array = []

for x in xrange :
    loss = loss_function(x)
    loss_array.append(loss)
    
ax.plot(xrange, loss_array)
ax.set_xlabel('x')
ax.set_ylabel('loss')

train_x = []
beta1 = 0.9
beta2 = 0.999
v = 0
s = 0

for i in range(100) :
    if i == 0 :
        pass
    else:
        ## Adam Optimizer
        dL_dx = loss_gradient(start_x)
        v = beta1*v + (1-beta1)*dL_dx
        s = beta2*s + (1-beta2)*dL_dx**2
        v_avg = v/(1-np.power(beta1, i))
        s_avg = s/(1-np.power(beta2, i))
        start_x = start_x - learning_rate*(1/(np.sqrt(s_avg)+1e-10))*v_avg
    train_x.append(start_x)
    
redDot, = ax.plot([], [], 'ro')

def animate(frame) :
    loss = loss_function(frame)
    redDot.set_data(frame, loss)
    return redDot

ani = FuncAnimation(fig, animate, frames=train_x)
FFwriter = animation.FFMpegWriter(fps=5)
ani.save('adam.gif')

adam.gif

  • 📌출처 : https://toyourlight.tistory.com/33(https://toyourlight.tistory.com/33)


  • ✨ 안장점 이슈
    • 안장점이란? “극대점”이자 “극소점”이 되는 구간 즉, 최소값이 아니지만 미분값이 0이 되는 지점

    image

3. 딥러닝 코드 구현

1) 딥러닝 학습과정 정리✨✨

  1. 다층 퍼셉트론을 구성하고, 실제 신경망의 임계값 대신 다양한 활성화 함수를 구성하여 비선형성을 갖춘다.
  2. 순전파의 과정을 통해 랜덤하게 배정된 각 가중치와 곱하여 예측값을 도출한다.
  3. 손실함수를 정의하여 실제값과 예측값의 차이를 규정한다.
  4. 역전파의 과정을 통해 각 가중치를 손실함수에 의거 각종 옵티마이저를 통해 전역적 극소점을 가지는 가중치로 업데이트 한다.

2) 코드구현 : tensorflow✨✨

  • 데이터셋 불러오기
    • tensorflow 제공 데이터 : 보스턴 집값
import tensorflow as tf

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.boston_housing.load_data()
x_train.shape, y_train.shape, x_test.shape, y_test.shape

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/boston_housing.npz
57026/57026 [==============================] - 0s 0us/step

((404, 13), (404,), (102, 13), (102,))


  • 신경망 구성하기
import tensorflow as tf

model = tf.keras.Sequential()
model.add(tf.keras.Input(shape=(13,))) # 입력층
model.add(tf.keras.layers.Dense(8, activation='relu')) # 노드 8개 은닉층, 활성화함수 : relu
model.add(tf.keras.layers.Dense(4, activation='relu')) # 노드 4개 은닉층, 활성화함수 : relu
model.add(tf.keras.layers.Dense(1, activation='relu')) # 출력층, 활성화함수 : relu
model.summary()

Model: "sequential_7"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_9 (Dense)             (None, 8)                 112       
                                                                 
 dense_10 (Dense)            (None, 4)                 36        
                                                                 
 dense_11 (Dense)            (None, 1)                 5         
                                                                 
=================================================================
Total params: 153 (612.00 Byte)
Trainable params: 153 (612.00 Byte)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________


  • Param : 각 레이어별 가중치 개수(bias(편향 미제거 기준)

    • (인풋(13) + 1) * 노드 개수(8) = 112

    • (이전 노드 개수(8) + 1) * 노드 개수(4) = 36

    • (이전 노드 개수(4) + 1) * 노드 개수(1) = 5


  • 컴파일 : 옵티마이저 설정, 손실함수 정의, metrics(평가요소) 설정
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3) ## 옵티마이저 : 아담, 학습률(1e-3)
lossfunction = 'mse' ## 손실함수 : Mean squared error
model.compile(optimizer=optimizer, loss=lossfunction, metrics=['mae', 'mse']) ## 옵티마이저, 손실함수 대입, 평가요소 설정(mae, mse)


  • 모델학습
history = model.fit(x_train, y_train, epochs=20) ## history 객체에 모델 학습결과 담기 / 학습횟수(epochs) 20회

Epoch 1/20
13/13 [==============================] - 0s 3ms/step - loss: 1093.3164 - mae: 18.4993 - mse: 1093.3164
Epoch 2/20
13/13 [==============================] - 0s 2ms/step - loss: 969.5359 - mae: 17.1256 - mse: 969.5359
Epoch 3/20
13/13 [==============================] - 0s 2ms/step - loss: 871.4448 - mae: 16.0362 - mse: 871.4448
Epoch 4/20
13/13 [==============================] - 0s 2ms/step - loss: 789.7881 - mae: 15.1139 - mse: 789.7881
Epoch 5/20
13/13 [==============================] - 0s 2ms/step - loss: 714.2711 - mae: 14.4676 - mse: 714.2711
Epoch 6/20
13/13 [==============================] - 0s 2ms/step - loss: 648.0341 - mae: 13.8079 - mse: 648.0341
Epoch 7/20
13/13 [==============================] - 0s 2ms/step - loss: 586.7796 - mae: 13.2222 - mse: 586.7796
Epoch 8/20
13/13 [==============================] - 0s 2ms/step - loss: 534.5012 - mae: 12.8259 - mse: 534.5012
Epoch 9/20
13/13 [==============================] - 0s 2ms/step - loss: 489.7008 - mae: 12.3977 - mse: 489.7008
Epoch 10/20
13/13 [==============================] - 0s 2ms/step - loss: 447.6282 - mae: 11.9009 - mse: 447.6282
Epoch 11/20
13/13 [==============================] - 0s 2ms/step - loss: 411.8113 - mae: 11.5876 - mse: 411.8113
Epoch 12/20
13/13 [==============================] - 0s 2ms/step - loss: 379.8321 - mae: 11.3213 - mse: 379.8321
Epoch 13/20
13/13 [==============================] - 0s 2ms/step - loss: 346.5337 - mae: 10.9670 - mse: 346.5337
Epoch 14/20
13/13 [==============================] - 0s 2ms/step - loss: 317.8628 - mae: 10.5855 - mse: 317.8628
Epoch 15/20
13/13 [==============================] - 0s 3ms/step - loss: 291.1151 - mae: 10.2904 - mse: 291.1151
Epoch 16/20
13/13 [==============================] - 0s 3ms/step - loss: 269.0137 - mae: 10.1115 - mse: 269.0137
Epoch 17/20
13/13 [==============================] - 0s 3ms/step - loss: 247.3324 - mae: 9.8335 - mse: 247.3324
Epoch 18/20
13/13 [==============================] - 0s 2ms/step - loss: 229.4131 - mae: 9.5082 - mse: 229.4131
Epoch 19/20
13/13 [==============================] - 0s 2ms/step - loss: 211.4243 - mae: 9.2610 - mse: 211.4243
Epoch 20/20
13/13 [==============================] - 0s 2ms/step - loss: 196.5922 - mae: 9.0761 - mse: 196.5922


  • MAE : Mean absolute error, MSE : Mean Squared error로 학습 결과 확인하기(로스함수 감소 확인)
plt.figure(figsize=(15,4))

plt.subplot(1,2,1)
plt.plot(history.history['mae'])
plt.title('Mean absolute error')
plt.ylabel('mae')
plt.xlabel('epochs')

plt.subplot(1,2,2)
plt.plot(history.history['mse'])
plt.title('Mean squared error')
plt.ylabel('mse')
plt.xlabel('epochs')
plt.show()


  • 실제값과 예측값 시각화 해보기
## x_test데이터로 예측값(y_pred) 도출
y_pred = model.predict(x_test)

## 예측값(y_pred)과 실제값(y_test) 비교
plt.title("predict vs target")
plt.scatter(np.arange(y_pred.shape[0]), y_pred, marker='x', label="model_predict")
plt.scatter(np.arange(y_test.shape[0]), y_test, marker='o', label="target")
plt.legend()
plt.show()

4/4 [==============================] - 0s 2ms/step

  • 비슷한 영역(0~60정도)에서 형성되는 것을 볼 수 있다.


  • 사전에 설정한 metrics로 모델 평가

    • MAE로 봤을 때, 약 8정도의 오차가 있는 것을 알 수 있다.
model.evaluate(x_test, y_test)

4/4 [==============================] - 0s 3ms/step - loss: 145.4071 - mae: 7.9725 - mse: 145.4071

[145.40708923339844, 7.972545146942139, 145.40708923339844]


3) 모델 평가 : 과소적합(Underfitting), 과적합(Overfitting)

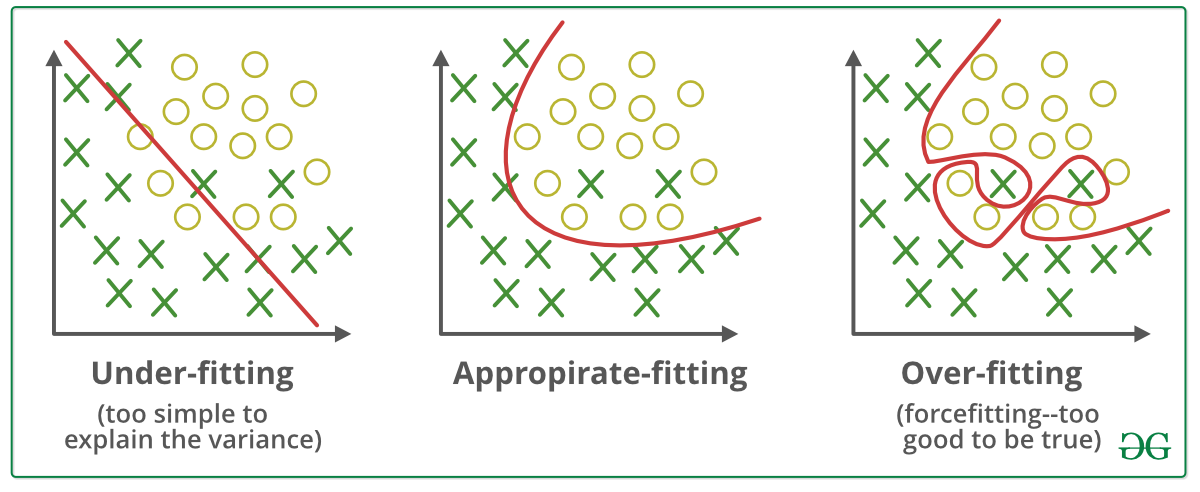
image


  • 과소적합 : (훈련 데이터에 대해서도) 설명력이 없는 모델
  • 과적합 : (훈련 데이터에 대해) 과하게 설명력이 있는 모델 → 일반화하기 힘든 모델
    • 이를 평가하고자 train data, test data를 구분해 평가한다.
    • epochs가 너무 적으면 과소적합, 너무 많으면 과적합 문제를 일으킨다.(모델에 따라 달라, 다수의 실험과 검증이 필요)
    • 과적합을 막기위해 일부 노드를 랜덤하게 삭제하는 Dropout을 사용하기도 한다.
    • 일반적으로 전체 데이터 셋의 하위 집합을 만들어 배치의 형태로 학습한다.
      1. 과적합 방지
      2. 메모리 사용 감소 → 학습 속도 향상
      3. 수렴 안정성 향상
    • 학습률, epochs과 같은 하이퍼 파라미터 조율을 위해서 추가적으로 validation data를 생성하기도 한다.


4. 정리 및 발전

  • 손실함수(Loss Function)은 모델에 따라 무엇을 정의해야할 지 다르다. 필요할 때 얼마든 지 자의적으로 조작 가능한 부분으로 보인다.
    • 분류모델 : Cross entrophy 등
    • 회귀모델 : MSE, MAE 등

  • 반면 옵티마이저(Optimizer)는 Adam이 가장 선호되나, SGD로도 극소점에 도달할 수 있다. 항상 안장점에 도달한 것이 아닐 지 주의가 필요하다.

  • 딥러닝의 기본적인 구조를 정리하였기에 다음엔 CNN, RNN, LSTM 등의 CV, NLP의 영역 뿐만 아니라 콜백(callback) 함수, 가중치 초기화, 배치 정규화, L1/L2규제, 전이 학습, KeraTuner, W&B 등 모델 학습 시 필요한 여러 도구들을 따로 정리해보고자 한다.

댓글남기기

참고

자격증 취득 후기 - SQLD, 빅데이터분석기사, 정보처리기사, 경영정보시각화능력(필기)

11 분 소요

본인 공부성향 원래부터 단순히 외우는 것을 잘하지 못했다. 항상 “왜”라는 물음을 통해 이해를 하는 것이 좋았고 능숙했다. 그래서 어렸을 때 단순하게 단어들을 외워야 했던 한문, 영어는 치가 떨릴만큼 싫어했고, 인과관계가 분명한 수학이나 사회, 과학을 좋아했었다. 그러다 ...