11 분 소요

1. CNN(Convolutional Neural Network)

(1 CNN의 주된 용도 : 이미지 처리

(1) 이미지 구조 확인하기

  • 흑백 이미지
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

## 흑백 이미지 불러오기
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() ## mnist 데이터셋 불러오기

print('형태 :', x_train[0].shape, '/ 최대값 :', x_train[0].reshape(-1).max(), '/ 최소값 :', x_train[0].reshape(-1).min()) ## 데이터 정보
plt.imshow(x_train[0], cmap='Greys') ## 시각화
plt.show()

형태 : (28, 28) / 최대값 : 255 / 최소값 : 0


  • 흑백 이미지란 결국 $x \times y$형태로 이루어진 matrix(행렬)


  • 그렇다면 우리가 일반적으로 접하는 여러 색을 입혀진 이미지는?
## 컬러 이미지 불러오기
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data() ## mnist 데이터셋 불러오기

print('형태 :', x_train[0].shape, '/ 최대값 :', x_train[0].reshape(-1).max(), '/ 최소값 :', x_train[0].reshape(-1).min()) ## 데이터 정보
plt.imshow(x_train[0]) ## 시각화
plt.show()

형태 : (32, 32, 3) / 최대값 : 255 / 최소값 : 0


  • 이미지는 $x \times y \times z$형태의 tensor(텐서)


(2) CNN이 고안된 이유

  • 이미지는 위치정보가 중요하다.→ 일반적인 MLP 모델로는 알수 없다.

    • 아래 코드를 통해 한줄로 펼쳐서 확인해보면 위에서 봤던 사진을 알아보기 힘들어짐 → 단순 MLP(Multi Layer Perceptron)으론 부적합

    • ☑️ 용어정리 : (32x32x3)의 형태에서 3은 각각 Red, Green, Blue인 RGB를 뜻하며 흔히 Depth 또는 Channel로 표현한다.

## 한줄로 펼쳐보기
plt.figure(figsize=(10,10))
plt.imshow(x_train[0].reshape(1,-1,3)[:,:64,:]) ## 64칸(2줄)까지만
ax = plt.gca()
ax.axes.xaxis.set_visible(False)
ax.axes.yaxis.set_visible(False)
plt.show()


2) 기본 구조

image


  1. feature 추출 구간
    • 입력층
    • Convolution Layer
    • Pooling Layer


  1. clasification 구간
    • Flatten(or Global Average Pooling)
    • Fully Conntected Layer
    • 출력층


3) feature 추출 구간

(1) 입력층 : shape를 맞추기

  • $(x, y, z)$의 형태로 입력하는 것이 필요(너비, 높이, 채널)

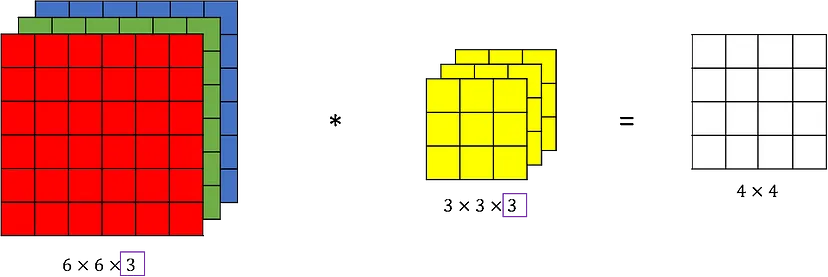
(2) Convolution Layer : Feature를 추출하는 층(feature map을 만드는 곳)

  • ✨연산과정 : 1개의 filter에선 feature map을 구성하는 1개의 depth가 나온다.(1개의 filter에 이미지의 depth 개수에 맞는 kernel이 형성).

    • filter의 갯수에 따라 다음 feature map의 depth가 결정됨.

    • 역전파시 kernel 내부의 숫자가 바로 가중치로 이를 업데이트

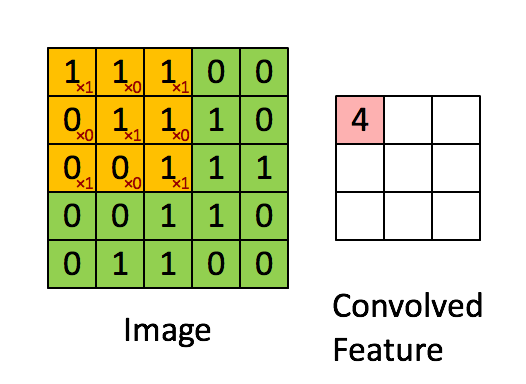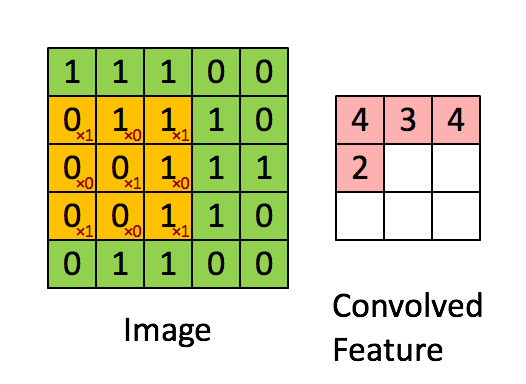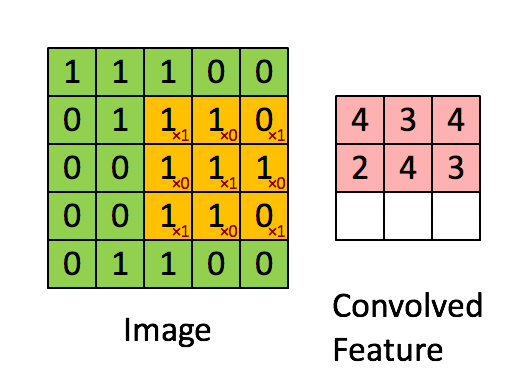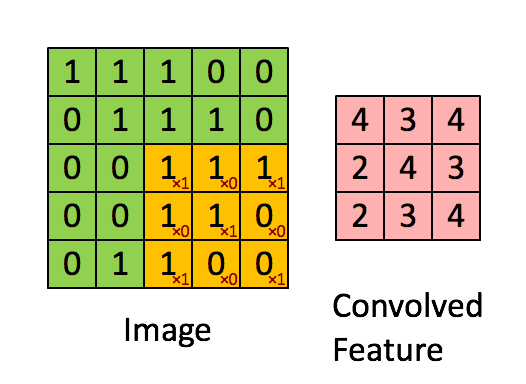
image

image


  • 여러 filter와 여러 kernel size가 필요한 이유 : kernel size에 따라 서로 다른 feature map이 도출됨.

    • filter개수 : 다양한 가중치로 이미지의 여러 특징들을 추출

    • kernel size : 작을 수록 작은 선의 특징이 추출되고, 클 수록 전체적인 형태가 추출

image


  • stride : 연산되는 커널의 보폭

image


  • padding : 빈칸을 추가해 feature map의 크기를 조절

image


  • stride, padding, kernel size에 결정되는 feature map의 높이 및 너비 구하는 식
$$ height = \frac{h - k + 2p}{s} + 1$$
$$ width = \frac{w - k + 2p}{s} + 1$$

h = 인풋 받는 tensor의 높이
w = 인풋 받는 tensor의 너비
k = kernel size(각각 높이, 너비)
p = padding
s = stride


(3) Pooling Layer : Feature를 요약하는 층(feature map 크기 축소)

  • 연산과정 : Max, Average 등의 기술통계를 이용하여 feature map의 크기를 축소를 해 연산량을 줄이고 불필요한 정보를 제거하는 역할을 한다.

    • 주로 Maxpooling을 Averagepooling보다 자주 쓴다. 말그대로 두드러진 feature을 더 잘살리기 위한 듯하다.

    • ✨ Pooling의 stride는 일반적으로 kernel size에 맞게 변형되나 다른 값으로 조정 가능하고 padding값 또한 적용 가능

image


4) clasification 구간

(1) Flatten Layer : 1차원 배열로 변경

  • MLP(Multi Layers Perceptron) 구조에 알맞게 수정

image


  • Global Average Pooling을 통해 1차원에 맞게 수정하기도 함(각 depth별 전체 평균값 활용)

image


(2) Fully Conntected Layer : 다층 퍼셉트론

  • classification을 위한 신경망 구성


(3) 출력층 : 결과 도출

  • 일반적으로 다중 클래스(softmax / 노드 개수 : 클래스 수), 이진 분류(sigmoid / 노드 개수 : 1)으로 구성됨


✨코드 구현

  • 모델구성
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() ## mnist 데이터셋 불러오기

## CNN 구성하기
model = tf.keras.models.Sequential([
                    ## 입력층(28,28,1), 32개 필터, 3x3 커널 사이즈, 렐루 활성화함수
                    tf.keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
                    ## 2x2 맥스풀링
                    tf.keras.layers.MaxPooling2D((2, 2)),
                    tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
                    tf.keras.layers.MaxPooling2D((2, 2)),
                    tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
                    tf.keras.layers.MaxPooling2D((2, 2)),
                    ## flatten
                    tf.keras.layers.Flatten(),
                    ## Fully-Conntected Layers
                    tf.keras.layers.Dense(64, activation='relu'),
                    ## 출력층
                    tf.keras.layers.Dense(10, activation='softmax')
])

model.summary()

Model: "sequential_2"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 conv2d_7 (Conv2D)           (None, 26, 26, 32)        320       
                                                                 
 max_pooling2d_4 (MaxPoolin  (None, 13, 13, 32)        0         
 g2D)                                                            
                                                                 
 conv2d_8 (Conv2D)           (None, 11, 11, 64)        18496     
                                                                 
 max_pooling2d_5 (MaxPoolin  (None, 5, 5, 64)          0         
 g2D)                                                            
                                                                 
 conv2d_9 (Conv2D)           (None, 3, 3, 64)          36928     
                                                                 
 max_pooling2d_6 (MaxPoolin  (None, 1, 1, 64)          0         
 g2D)                                                            
                                                                 
 flatten_2 (Flatten)         (None, 64)                0         
                                                                 
 dense_4 (Dense)             (None, 64)                4160      
                                                                 
 dense_5 (Dense)             (None, 10)                650       
                                                                 
=================================================================
Total params: 60554 (236.54 KB)
Trainable params: 60554 (236.54 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________


  • 파라미터(가중치 + 편향) 수 계산
$$ W_{c} = K^{2} \times C \times N$$
$$ B_{c} = N$$
$$ P_{c} = W_{c} + B_{c}$$

$W_{c}$ : 가중치 개수
$B_{c}$ : 편향 개수
$P_{c}$ : 파라미터 개수
K : 커널 사이즈(너비와 높이가 같다고 가정)
C : 인풋 tensor의 channel 개수
N : 필터의 개수


  1. conv2d_7 / 320 = 3x3x1x32+32

  2. conv2d_8 / 18496 = 3x3x32x64+64

  3. conv2d_9 / 36928 = 3x3x64x64+64

  4. dense_4 / 4160 = 64x(64+1)

  5. dense_5 / 650 = 10x(64+1)


  • 옵티마이저, 손실함수, 평가요소 지정
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])


  • 학습
history = model.fit(x_train, y_train, validation_split=0.2, epochs=10) ## 20%자료는 validation 데이터로 활용

Epoch 1/10
1500/1500 [==============================] - 10s 7ms/step - loss: 0.0299 - accuracy: 0.9901 - val_loss: 0.0237 - val_accuracy: 0.9937
Epoch 2/10
1500/1500 [==============================] - 10s 7ms/step - loss: 0.0260 - accuracy: 0.9921 - val_loss: 0.0267 - val_accuracy: 0.9924
Epoch 3/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0240 - accuracy: 0.9923 - val_loss: 0.0459 - val_accuracy: 0.9878
Epoch 4/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0224 - accuracy: 0.9933 - val_loss: 0.0328 - val_accuracy: 0.9914
Epoch 5/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0204 - accuracy: 0.9939 - val_loss: 0.0440 - val_accuracy: 0.9902
Epoch 6/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0220 - accuracy: 0.9938 - val_loss: 0.0569 - val_accuracy: 0.9858
Epoch 7/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0198 - accuracy: 0.9945 - val_loss: 0.0482 - val_accuracy: 0.9903
Epoch 8/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0240 - accuracy: 0.9933 - val_loss: 0.0489 - val_accuracy: 0.9887
Epoch 9/10
1500/1500 [==============================] - 9s 6ms/step - loss: 0.0154 - accuracy: 0.9953 - val_loss: 0.0617 - val_accuracy: 0.9864
Epoch 10/10
1500/1500 [==============================] - 10s 7ms/step - loss: 0.0220 - accuracy: 0.9939 - val_loss: 0.0764 - val_accuracy: 0.9858


  • 학습결과 시각화
plt.figure(figsize=(12,3))
plt.subplot(1,2,1)
plt.title('accuracy and val_accuracy')
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label='val_accuracy')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()

plt.subplot(1,2,2)
plt.title('loss and val_loss')
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend()
plt.show()

  • val_accuracy가 학습할수록 떨어지는 상황으로 보아 과적합의 가능성이 있다.

    • 과적합을 해소하고자 차 후 언급할 dropout, L1/L2규제,학습률 조정 등 다양한 방식을 이용한다.


  • 평가
model.evaluate(x_test, y_test)

313/313 [==============================] - 1s 2ms/step - loss: 0.1289 - accuracy: 0.9804

[0.12889517843723297, 0.980400025844574]


  • test_data를 활용해 확인해본 결과 0.9804 정도의 정확도를 얻을 수 있었다. validation accuracy였던 0.9858보다도 낮은 것으로 보아, 과적합 가능성이 높아보인다.


2. RNN(Recurrent Neural Network)

1) Sequence(시퀀스)란?

  • Sequence(시퀀스) : 순서가 있는 데이터(텍스트, 시계열 데이터, 영상, 음성 등)

  • Sequence model의 종류

    1. one to one

    2. one to many

      • 예시 : 이미지 데이터에서 설명글 출력(Image → Text)

    3. many to one

      • 예시 : 감성 분석, 주가 분석, 시계열 예측 등

    4. many to many(encoder → decoder)

      • 예시 : 영어, 한국어로 번역

    5. many to many

      • 예시 : TEXT에서 언급된 사람, 회사, 장소 등의 개체 인식하여 출력

image


2) RNN의 구조

image


  • Input$(x_{0}, x_{1},…,x_{t})$
  • hidden state$(h_{0}, h_{1},…,h_{t})$
  • output(hidden state를 이용해 출력해낼 $y$)


image


  • ✨✨과거의 state($h_{t-1}$)와 새로운 인풋 값($x_{t}$) 받아 다음의 hidden state를 정의($h_{t}$), hidden state($h_{1}, h_{2},…,h_{t}$)를 이용해 $y$ 출력


$$h_{t} = tanh(W_{hh}h_{t-1} + W_{xh}x_{t})$$
$$y_{t} = softmax(W_{hy}h_{t})$$

t : 시점
h : hidden state
$W_{hh}$ : tanh함수에서의 hidden state의 가중치
x : 인풋 값
$W_{xh}$ : tanh함수에서의 hidden state의 가중치
y : 출력값
$W_{hy}$ : softmax함수에서의 hidden state의 가중치


✨ 한계 : 장기 의존성 문제

  • LongTerm Dependencies : t가 커질수록(층이 커질수록 $\approx$ 시점이 길어질수록) 앞 쪽의 정보 손실(Vanishing Gradient $\approx$ 가중치 업데이트가 잘 안됨)이 커짐 → 보완하고자 LSTM 모델이 나옴


3) LSTM(Long Short-Term Memory) : 전통 RNN의 개선모델

image


(1) ✨Cell State : Vanishing Gradient 해소하기 위한 state pipeline

image


(2) Forget Gate : 과거의 정보 망각정도 결정(Sigmoid)

  • Sigmoid함수를 통해 0~1 사이의 값을 반환함(망각정도)

image


(3) Input Gate : 기억할 현재 정보 결정(Sigmoid * tanh)

  • Sigmoid함수를 통해 0~1 사이의 값을 반환(기억정도), 이전 hidden state인 $h_{t-1}$과 이번 인풋 값 $x_{t}$를 통해 만들어진 $\tilde{C_{t}}$와 곱해져 기억할 정보 결정

image


(4) Update : 새로운 cell state 업데이트

  • Forget Gate에서 결정된 망각정도와 과거의 cell state가 곱해져 $f_{t} * C_{t-1}$ , Input Gate에서 배출된 $i_{t} * \tilde{C_{t}}$ 이 더해져 새로운 cell state인 $C_{t}$가 결정

image


(5) Output Gate : hidden state값을 결정하기 위해 cell sate값을 얼마나 활용할 것인지 결정

image


✨코드 구현

  • 주가 데이터를 활용하여 5일 간의 주가 데이터 : x로 다음 날 주가 : y를 예측하는 모델을 만들어보고자 합니다.

    • 학습 데이터 : 2015-01-01 ~ 2021-12-31

    • 테스트 데이터 : 2022-01-01 ~ 2023-12-31

    • 활용 모델 : LSTM


  • 데이터 받기
import yfinance as yf # yahoo finance 제공 데이터 접근 가능

## 시계열 데이터 주가정보
AMZN = yf.download('AMZN',
                  start = '2015-01-01',
                  end = '2023-12-31',
                  progress = False)

all_data = AMZN[['Adj Close', 'Open', 'High', 'Low', 'Close', 'Volume']].round(2)
all_data.head(10)
Adj Close Open High Low Close Volume
Date
2015-01-02 15.43 15.63 15.74 15.35 15.43 55664000
2015-01-05 15.11 15.35 15.42 15.04 15.11 55484000
2015-01-06 14.76 15.11 15.15 14.62 14.76 70380000
2015-01-07 14.92 14.88 15.06 14.77 14.92 52806000
2015-01-08 15.02 15.02 15.16 14.81 15.02 61768000
2015-01-09 14.85 15.07 15.14 14.83 14.85 51848000
2015-01-12 14.57 14.88 14.93 14.46 14.57 68428000
2015-01-13 14.74 14.87 15.07 14.66 14.74 82728000
2015-01-14 14.66 14.60 14.80 14.32 14.66 110774000
2015-01-15 14.35 14.70 14.80 14.34 14.35 88384000


  • 데이터 전처리

    • 5일전까지의 주가 : x 학습 파일

    • 해당일 주가 : y 타겟 파일

# Adj Close데이터 추출
data = AMZN[['Adj Close']]

# 학습데이터(전 5일간)
x = []
# 타겟데이터(주가 데이터)
y = []
# 날짜
index = []

# 데이터 가공
for i in range(len(data)-5) :
    x.append(data.iloc[i:5+i].values.reshape(-1))
    y.append(data.iloc[5+i].values[0])
    index.append(data.iloc[5+i].name)

x = np.array(x)
y = np.array(y).reshape(-1, 1)
index = list(map(lambda x : str(x), index))

x.shape, y.shape

((2259, 5), (2259, 1))


  • Scale

    • MinMaxScale : 0~1사이 숫자로 변환
# 스케일링
from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
x = scaler.fit_transform(x)

scaler2 = MinMaxScaler()
y = scaler2.fit_transform(y)


  • 훈련, 테스트 데이터셋 split

    • 2022이전 : 훈련 데이터

    • 2022이후 : 테스트 데이터

split_number = index.index('2022-01-03 00:00:00') ## 2022년 전후 분기
x_train = x[:split_number].reshape(-1,5,1)
y_train = y[:split_number].reshape(-1,1,1)
x_test = x[split_number:].reshape(-1,5,1)
y_test = y[split_number:].reshape(-1,1,1)
index_test = index[split_number:]
index_test = np.array(list(map(lambda x:x.replace(' 00:00:00',''), index_test)))

x_train.shape, x_test.shape

((1758, 5, 1), (501, 5, 1))


  • 모델구성
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.LSTM(units = 32,
                               return_sequences = True,
                               input_shape = (x_train.shape[1], 1),
                               activation = 'tanh'
))
model.add(tf.keras.layers.LSTM(units = 16, activation = 'tanh'))
model.add(tf.keras.layers.Dense(units = 1, activation = 'sigmoid')) # minmaxscale을 해서
model.summary()

Model: "sequential_19"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 lstm_22 (LSTM)              (None, 5, 32)             4352      
                                                                 
 lstm_23 (LSTM)              (None, 16)                3136      
                                                                 
 dense_8 (Dense)             (None, 1)                 17        
                                                                 
=================================================================
Total params: 7505 (29.32 KB)
Trainable params: 7505 (29.32 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________


  • 모델 컴파일
model.compile(optimizer=tf.keras.optimizers.Adam(),
             loss = 'mse',
             metrics=['mse', 'mae'])


  • 모델 학습
history = model.fit(x_test, y_test, validation_split=0.2, epochs=20)

Epoch 1/20
13/13 [==============================] - 4s 61ms/step - loss: 0.0230 - mse: 0.0230 - mae: 0.1179 - val_loss: 0.0239 - val_mse: 0.0239 - val_mae: 0.1475
Epoch 2/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0141 - mse: 0.0141 - mae: 0.0976 - val_loss: 0.0064 - val_mse: 0.0064 - val_mae: 0.0686
Epoch 3/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0135 - mse: 0.0135 - mae: 0.0985 - val_loss: 0.0064 - val_mse: 0.0064 - val_mae: 0.0684
Epoch 4/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0123 - mse: 0.0123 - mae: 0.0935 - val_loss: 0.0096 - val_mse: 0.0096 - val_mae: 0.0887
Epoch 5/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0115 - mse: 0.0115 - mae: 0.0903 - val_loss: 0.0061 - val_mse: 0.0061 - val_mae: 0.0681
Epoch 6/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0102 - mse: 0.0102 - mae: 0.0853 - val_loss: 0.0055 - val_mse: 0.0055 - val_mae: 0.0645
Epoch 7/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0088 - mse: 0.0088 - mae: 0.0789 - val_loss: 0.0042 - val_mse: 0.0042 - val_mae: 0.0557
Epoch 8/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0069 - mse: 0.0069 - mae: 0.0694 - val_loss: 0.0025 - val_mse: 0.0025 - val_mae: 0.0432
Epoch 9/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0047 - mse: 0.0047 - mae: 0.0568 - val_loss: 0.0024 - val_mse: 0.0024 - val_mae: 0.0436
Epoch 10/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0028 - mse: 0.0028 - mae: 0.0435 - val_loss: 0.0011 - val_mse: 0.0011 - val_mae: 0.0279
Epoch 11/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0018 - mse: 0.0018 - mae: 0.0341 - val_loss: 0.0013 - val_mse: 0.0013 - val_mae: 0.0305
Epoch 12/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0309 - val_loss: 7.0903e-04 - val_mse: 7.0903e-04 - val_mae: 0.0203
Epoch 13/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0310 - val_loss: 6.7931e-04 - val_mse: 6.7931e-04 - val_mae: 0.0196
Epoch 14/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0304 - val_loss: 0.0017 - val_mse: 0.0017 - val_mae: 0.0353
Epoch 15/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0305 - val_loss: 6.8952e-04 - val_mse: 6.8952e-04 - val_mae: 0.0196
Epoch 16/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0308 - val_loss: 6.3063e-04 - val_mse: 6.3063e-04 - val_mae: 0.0186
Epoch 17/20
13/13 [==============================] - 0s 8ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0304 - val_loss: 6.4388e-04 - val_mse: 6.4388e-04 - val_mae: 0.0189
Epoch 18/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0301 - val_loss: 7.8488e-04 - val_mse: 7.8488e-04 - val_mae: 0.0216
Epoch 19/20
13/13 [==============================] - 0s 7ms/step - loss: 0.0014 - mse: 0.0014 - mae: 0.0299 - val_loss: 6.9018e-04 - val_mse: 6.9018e-04 - val_mae: 0.0197
Epoch 20/20
13/13 [==============================] - 0s 8ms/step - loss: 0.0015 - mse: 0.0015 - mae: 0.0302 - val_loss: 6.5676e-04 - val_mse: 6.5676e-04 - val_mae: 0.0190


  • 모델 평가
plt.figure(figsize=(15,4))
plt.subplot(1,2,1)
plt.title("Mean Absolute error")
plt.grid()
plt.xlabel('epochs')
plt.ylabel('mae')
plt.plot(history.history['mae'], label='train')
plt.plot(history.history['val_mae'], label='validation')
plt.legend()

plt.subplot(1,2,2)
plt.title("Mean Squared error")
plt.grid()
plt.xlabel('epochs')
plt.ylabel('mse')
plt.plot(history.history['mse'], label='train')
plt.plot(history.history['val_mse'], label='validation')
plt.legend()
plt.show()


model.evaluate(x_test, y_test)

16/16 [==============================] - 0s 2ms/step - loss: 0.0013 - mse: 0.0013 - mae: 0.0273

[0.0012504284968599677, 0.0012504284968599677, 0.027338067069649696]

y_pred = model.predict(x_test)

plt.figure(figsize=(15,4))
plt.plot(y_pred, label='predict')
plt.plot(y_test.reshape(-1), label='real')
plt.legend()
plt.show()

16/16 [==============================] - 1s 2ms/step


  • 그래프로 보다시피 실제 주가와 예측 주가가 비슷한 경향을 띄는 것으로 보아 예측이 어느정도 성공적인 것으로 보인다. 그만큼 시계열 데이터에서 LSTM모델이 효율적이다는 사실을 깨달을 수 있었다.

댓글남기기

참고

자격증 취득 후기 - SQLD, 빅데이터분석기사, 정보처리기사, 경영정보시각화능력(필기)

11 분 소요

본인 공부성향 원래부터 단순히 외우는 것을 잘하지 못했다. 항상 “왜”라는 물음을 통해 이해를 하는 것이 좋았고 능숙했다. 그래서 어렸을 때 단순하게 단어들을 외워야 했던 한문, 영어는 치가 떨릴만큼 싫어했고, 인과관계가 분명한 수학이나 사회, 과학을 좋아했었다. 그러다 ...