Scikit-learn(지도학습2) - 회귀

1. 회귀 분석이란 무엇인가?

• 통계학에서 회귀 분석(回歸分析, 영어: regression analysis)은 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤 적합도를 측정해 내는 분석 방법

✨데이터 불러오기

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes # 당뇨병 환자 데이터
def make_dataset():
    dataset = load_diabetes()
    df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
    df['target'] = dataset.target
    X_train, X_test, y_train, y_test = train_test_split(
        df.drop('target', axis=1), df['target'], test_size=0.2, random_state=1004)
    return X_train, X_test, y_train, y_test

X_train, X_test, y_train, y_test = make_dataset()

2. 선형 회귀(LinearRegression)

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train) # 학습 데이터 학습
pred = model.predict(X_test) # 테스트 데이터로 예측값 도출

• 데이터를 학습한 선형 회귀 모델을 생성하여, 검증 데이터를 통해 예측값(pred)를 생성한다.

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, pred)

• MSE(Mean Squared Error) 값을 통해 모델을 평가한다. MSE는 수치가 작을수록 좋은 모델이라는 뜻이다. 그렇다면 여기서 MSE는 어떻게 산출되는 것인가? 그를 위해 error의 정의를 먼저 알아보도록 하자.

MSE 값 : 2707.6318521641583

• 여기서 Error 란 실제값과 예측값의 차이라고 보면 된다. 아래 그림을 보면 더욱 이해가 잘 갈것이다.

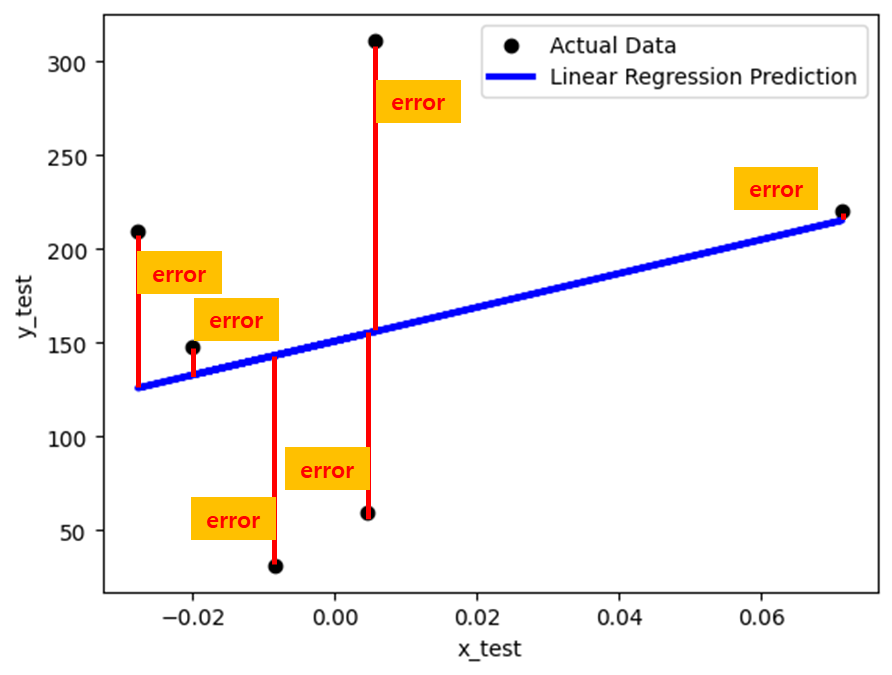
단순 선형 회귀 분석 모델의 error들

• 해당 error값들을 활용하여 선형 회귀 모델을 평가하는 방법들은 다음과 같이 있다.

✨ 회귀 모델 검증 방법들

1, 2은 값이 작을수록 모델의 설명력이 좋고, 3, 4는 1에 가까울수록 모델의 설명력이 좋다

• 이 외에도 MSE에 단순히 ROOT를 씌워 MSE에 Root를 씌워서 사용하기도 한다.

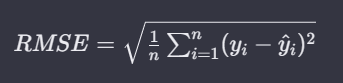
Root Mean Squared Error

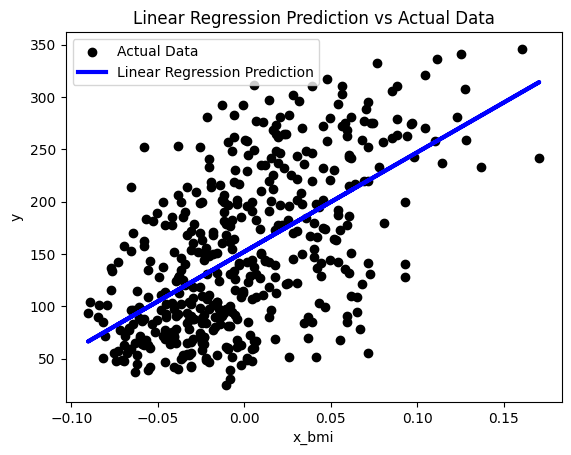
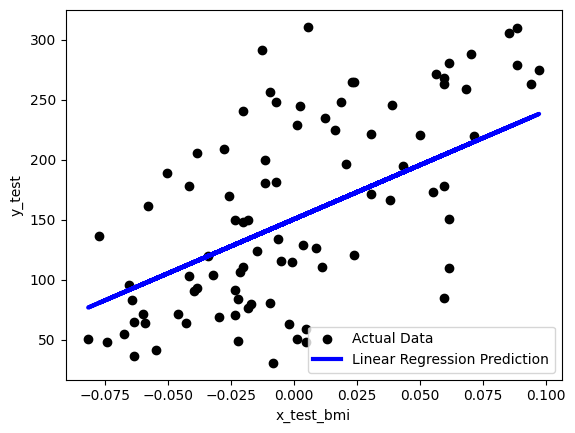
하지만 해당 코드를 통해 생성한 모델을 시각화를 해보면 일반적으로 기대하던 선형과는 다른 모습을 가진다.

import matplotlib.pyplot as plt

plt.scatter(X_test["bmi"], y_test, color='black', label='Actual Data')
plt.plot(X_test["bmi"], pred, color='blue', linewidth=3, label='Linear Regression Prediction')
plt.xlabel('x_test_bmi')
plt.ylabel('y_test')
plt.legend()
plt.show()

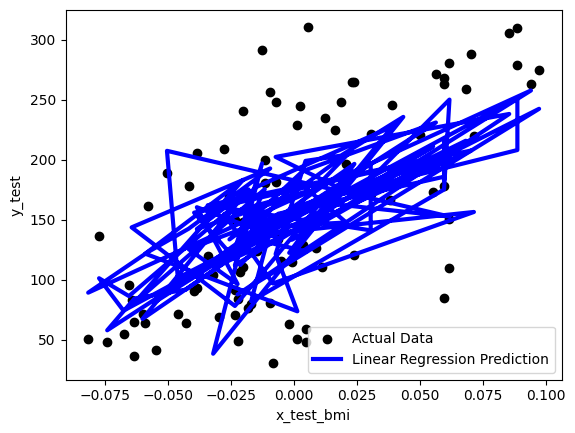
bmi특성을 기준으로 그린 모델

2차원 그래프이기에 하나의 특성과 결과만을 가지고 그려보면 선형의 모습이 아니다. 왜냐하면 우리들의 데이터는 하나의 특성만으로 만든 모델이 아니라, 여러 가지 특성을 활용해 그린 모델이기 때문이다.

즉, 단순 회귀 모델이 아닌,

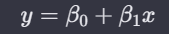
단순 선형 회귀 모델

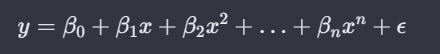
다항 회귀 모델(Polynomial Regression)

다항 회귀 모델이기 때문에 발생하는 현상이다. 때문에, 모델 fit을 bmi 특성만을 가지고 진행한다면 기대하던 선형 모델의 모양을 볼 수 있다.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

model = LinearRegression()
model.fit(X_train[["bmi"]], y_train)
pred = model.predict(X_test[["bmi"]])

bmi특성만을 가지고 예측한 모델

이러한 특성을 이해하고 "전진 선택법(Forward Selection)"과 "후진 소거법(Backward Elimination)"을 이해하면 좋다. 즉 말 그대로 주어진 모델에서 X1 ~ Xk에서 특성을 추가하거나 제거함으로써 error의 값을 줄여나가며 모델의 정확도를 올려나가거나 과적합(overfitting) 문제를 해소한다.

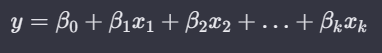
주어진 모델 예시

하지만, 이 방법과 달리 특성을 제거하거나 추가하지 않고 모델을 개선하기 위해 나온 회귀 모델 또한 있다. 바로 라쏘(Lasso)와 릿지(Ridge)입니다. 이는 각각 규제방식으로 L1(절대값을 패널티항으로), L2(제곱값을 패널티항으로)을 이용합니다. 규제를 한다는 것은 가중치 또는 계수(위 식에서는 β들을 일컫는다)의 값을 낮추면서 과적합을 방지하고 일부 특성의 영향을 줄이기 위해 사용되는 방법들입니다. 이해 안가시더라도 아래를 보시면 조금 이해가 가실 겁니다.

3. 라쏘(Lasso) 회귀 vs 릿지(Ridge)

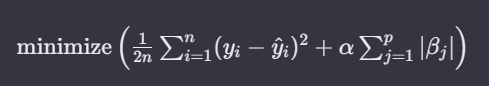
라쏘 회귀 수식

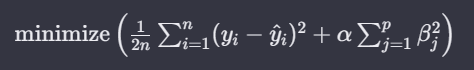
릿지 회귀 수식

일단 두가지 모델을 시각화 해보면 규제의 의미를 쉽게 판단할 수 있을 것입니다.

from sklearn.linear_model import Lasso
model = Lasso(alpha = 0.5)
#model = Lasso(alpha = 1.5)
model.fit(X_train, y_train)
pred = model.predict(X_test)

from sklearn.linear_model import Ridge
model = Ridge(alpha=1.5)
#model = Ridge(alpha=10)
model.fit(X_train, y_train)
pred = model.predict(X_test)

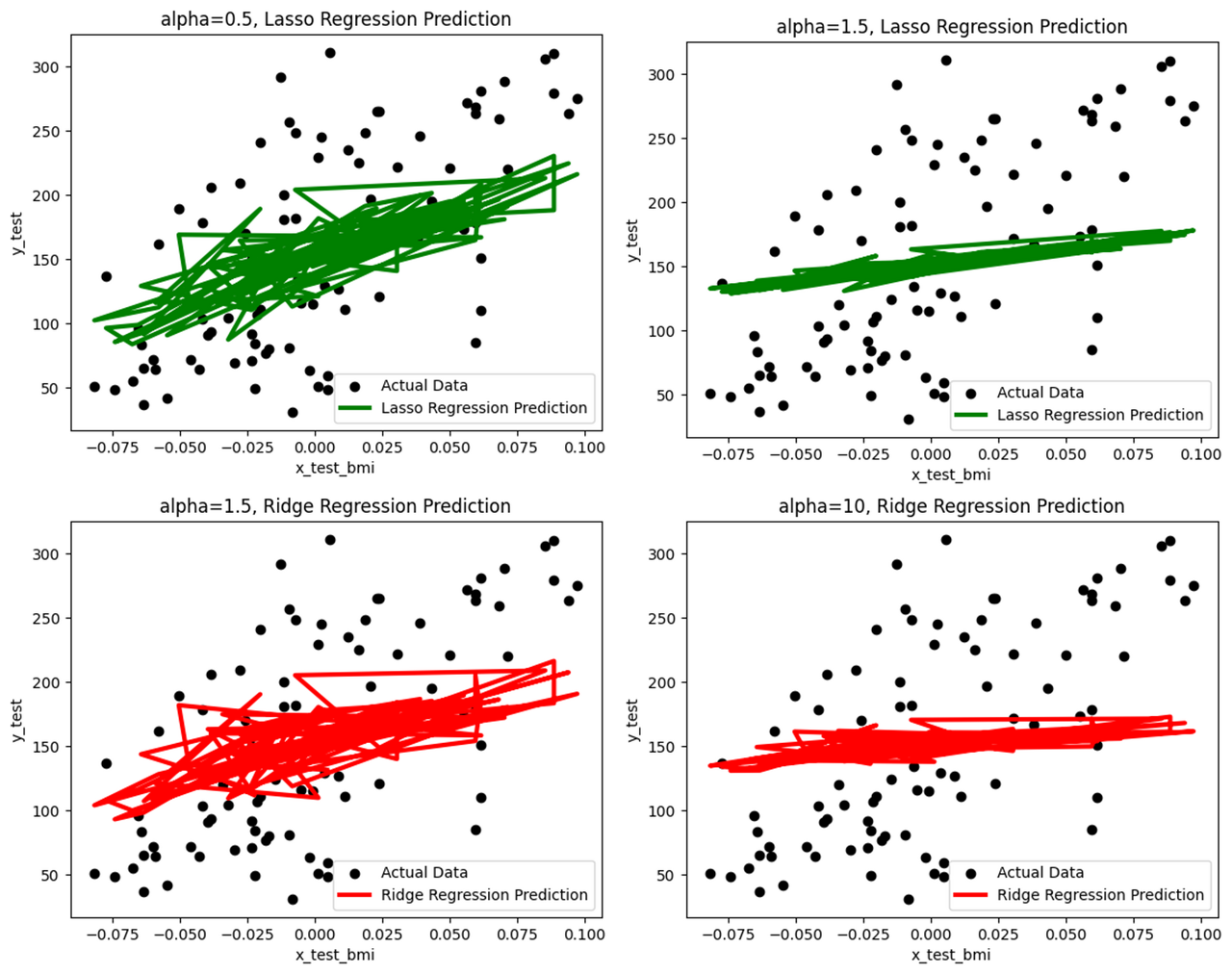
위 라쏘(alpha 0.5, 1.5), 아래 릿지(alpha 1.5, 10)

alpha값은 모델의 규제의 정도이다. 라쏘는 적은 수치에도 일찍 선형 모양을 갖추는 반면, 릿지는 강도가 10까지 도달해야 선형의 모습을 갖추는 것처럼 보이나, 기울기가 더 낮다. 즉, 라쏘는 다른 특성들의 영향력을 일찍이 없애는 반면 릿지는 전체적인 계수를 낮춘다고 이해하는 것이 좋습니다. 이해를 돕고자 chat-gpt의 설명을 넣겠습니다.

라쏘는 여러 특성들의 계수를 0으로 만드는 반면, 릿지는 그렇지 않다. 때문에, 라쏘는 빠르게 선형의 모습을 갖추는 것{: style=”text-align: center;”}

고로 각자 아래와 같은 상황에 이용하게 된다.

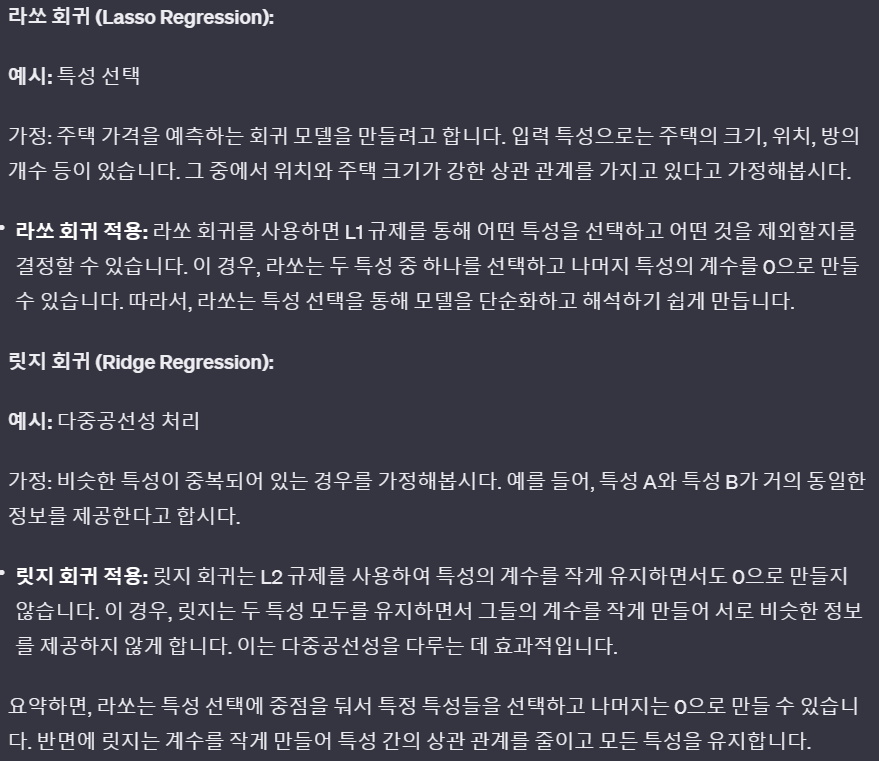
출처 : chat-gpt

물론 서로 다르기 때문에, 둘의 기능을 함께 고려한 엘라스틱넷 (Elsatic-net) 회귀도 존재한다. 간단히 코드로만 소개하겠다.

4. 엘라스틱넷 회귀(Elsatic-net)

from sklearn.linear_model import ElasticNet
model = ElasticNet(alpha=1, l1_ratio=0.5)  # alpha는 규제의 정도, l1_ratio는 라쏘 회귀의 정도
model.fit(X_train, y_train)
pred = model.predict(X_test)

추가적인 하이퍼 파라미터로 l1_ratio가 주어지는데 말그대로 라쏘 적용 비율이라 생각하면 좋다.

5. 랜덤 포레스트(RandomForest) vs XGBoost(eXtreme Gradient Boosting)

앞선 분류를 보고 왔으면 두 가지 또한 마찬가지 방식을 차용한다. 앙상블 기법으로서 랜덤 포레스트는 배깅을 활용하고, XGBoost는 Gradient Boosting기법을 사용하여 이전의 모델을 보완하는 방식을 이용한다. 코드만 간단히 소개하겠다.

• 랜덤 포레스트 코드

from sklearn.ensemble import RandomForestRegressor
model_r = RandomForestRegressor() # n_estimators의 기본값은 10
model_r.fit(X_train, y_train)
pred_r = model_r.predict(X_test)

• XGBoost 코드

from xgboost import XGBRegressor
model_x = XGBRegressor(n_estimators=100) # n_estimators의 기본값은 10
model_x.fit(X_train, y_train)
pred_x = model_x.predict(X_test)